Bitcoin is a tremendous experiment. Here we have a ledger that is open for everyone to inspect and use. Because every transaction is recorded, the potential for data mining is nearly unlimited. Today’s post will do some data mining, but on a very limited scale. This will be a relatively long post and will be heavy in theory and math. Of course you can skip all the “blahh, blahh blahh, math, blah, blah.” and just look at the pretty pictures. Included in today’s post are the ~1-hour (6 blocks) averaged data files and the Matlab source code. To use the Matlab source, you will need a parsed blockchain database, I used bitcoin-abe v0.9 compiled under Mac OS 10.9.2 to create a MySQL database. I can’t make the database available because my ISP would hate me, and there is not enough space on my WordPress account.
I develop a measure of marginal utility of bitcoin from the time needed to find each block. This is simply the estimated network hash rate divided by the total coinbase for that interval. The difficulty is in arriving at this relationship. To do this, I used the complementary relationship of time and the Hamiltonian (utility). Armed with the understanding of the relationship of time to utility, we use the time to discover a new block as the measure of the utility gained by the discovery. The effort of the miners to discover the coinbase is the marginal power [TH/BTC-s] needed to maintain the miners’ operations. We will expand later the relationship of a TH/s to the MW. We can choose to leave the network power as a non dimensional quantity, using difficulty in lieu of hash rate. For the sake of making clearer analogies, we will use the dimensional form.
The Uncertainty Principle
Werner Heisenberg as part of his PhD thesis developed the relationship between our knowledge of the complementary measures of a system. His work focused on a particles position and momentum. While we are not dealing with particles or of position in real space or momentum in real space, we are dealing with measurable space. The blockchain contains a record of every transaction. We can in theory and in practice count these transactions, allowing us to apply the principles of statistical inference to the data that we have at hand. I began in Elementary Principles of Statistical Economics by showing how to use the time evolution of a probability density of state with a Hamiltonian. The Hamiltonian is merely an operator and if it exists for a space then under the uncertainty principle there exists a complementary measure, time. John Baez has an interesting post that explores the concept of the relationship between time and the Hamiltonian.
The time stamp of the block creation time is not a precise measure. There is a great deal of uncertainty behind the measure due to the constraints in the code for permissible time stamps. Because of this uncertainty, we cannot precisely know the time . We measure time
. We describe the uncertainty principle as,
(1)
At the classical limit, we find that the fluctuation of the Hamiltonian, is inversely proportional to the fluctuation in measured time,
. Using this limit we measure the fluctuation of the Hamiltonian as proportional to the inverse of the change in measured time.
(2)
Quantifying Intensive Measures
Our attention now turns to measuring the intensive parameters of the system defined by the bloakchain. We develop measures first for pressure and then for temperature.
bitcoin pressure
When we include the coinbase of each block we find the measure of the marginal utility, pressure, of bitcoin. The marginal utility of bitcoin is defined as,
(3)
I apologize for the variable confusion. When we typically talk about utility we use . To this point I followed the convention of physics that when we describe the internal energy/utility,
, in quantum contexts we refer to it as the operator
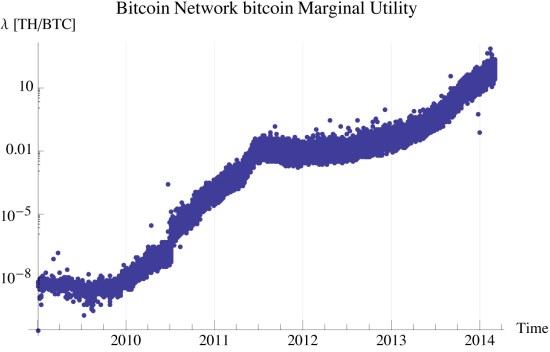
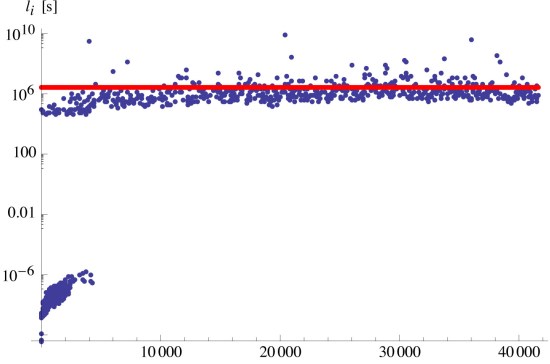
. Under the constraints of Bitcoin, miners work for a specific payout of bitcoins, the coinbase. How hard they work to do this is the time taken to discover the next block. In this context, mining acts to determine the marginal utility of finding the next bitcoin. Figure 1 shows the marginal utility of bticoin measured, using the aggregate information every 6 blocks, approximately hourly. The study period is from the genesis block through block 289207. We express the units of bitcoin pressure as TH/BTC, terahash/bitcoin.
bitcoin specific internal utility
The internal utility of the Bitcoin network is not an intensive/endogenous measure. It is an extensive/exogenous measure. Later, I will show how it is proportional to the temperature (an intensive measure). This requires an assumption of a certain utility function, which at this point limits the generality of the approach. We will therefor avoid such consideration until we have the theoretical measures developed.
We note that the distribution of bitcoin transactions is most closely represented by the log-normal distribution. I looked at both and
.
provided the best representation as there can be only one change address when using a wallet based on the reference wallet implementation. While transactions occur discretely and are integers of satoshi, there is enough division with them and especially later enough transactions (>30/6 blocks) to approximate the system classically as a continuous distribution. Only in the first year, when there aren’t enough transactions that this assumption breaks down. The recent years, of which we are concerned, this assumption holds relatively well.
The temperature of a log normal distribution is the expectation of over each integration period. I showed this in Various Properties of the Log-Normal Distribution. We determine this by:
(4)
We compute and
using the MLE estimates for a log-normally distributed variable.
This is expectation is related to specific internal utility, . The units of the expectation are measured in BTC, not in units of utility. To convert to utility we let:
Figure 2 shows the specific internal utility with units of TH.
bitcoin participant potential
The statistic of the log-normal distribution has a component of variance that is independent of location,
. When we rearrange the entropy in terms of
,
, and
we have,
We define a new parameter which is a form of the Lambert
function. For
,
.
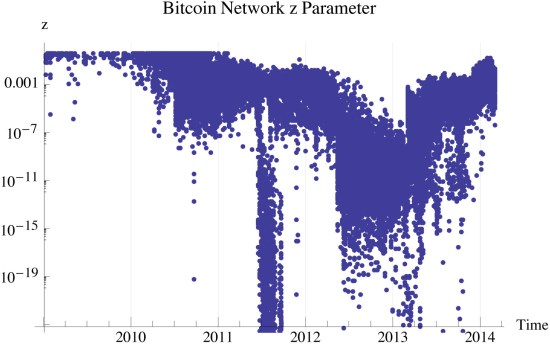
describes the distance of the system from the maximum entropic carrying capacity. Systems of relatively low density have
. Systems of relatively high density have
. Figure 3 shows three distinct phases of the bitcoin network, inception, expansion, and our current maturation. Bitcoin will likely reach an equilibrium of
which maximizes the networks entropy for any given utility and total satoshi’s. With bitcoin transactions being log-normally distributed, the
potential,
. At the point of maximum entropy,
.
The phases of bitcoin, remind me of evolutionary history. When life first appeared there were very few forms, early adopters if you will that existed in what can best be thought of as quantum states of very low biodiversity. The expansion phase is akin to the Cambrian Explosion, where life tried every combination it could think of causing a very low density of states, . Life on the planet then went through a consolidation phase where many of the life forms that were tried out became extinct as they couldn’t compete with the more capable life forms. Life on the planet then came back to an equilibrium where
. The density of life then appears to follow the constraints based upon planet, including several ice ages, and 5 major extinction events. Species diversity today appears to follow a canonical log-normal distribution where
. Bitcoin appears to be well within its adolescence, and is not yet fully mature.
Maturity has several equivalent definitions. First is . Another is when the maximum potential of participants is reached,
. Just like what appears to be the case with life on the planet, the maximum entropic carrying capacity is not fixed.

Figure 4: Phanerozoic biodiversity as shown by the fossil record. Source Wikipedia
Quantifying Extensive Measures
We now turn our focus to the logically independent extensive parameters money supply , utility
, and number of unique participants
. Please note that
is a function of
. We begin with the simplest to measure,
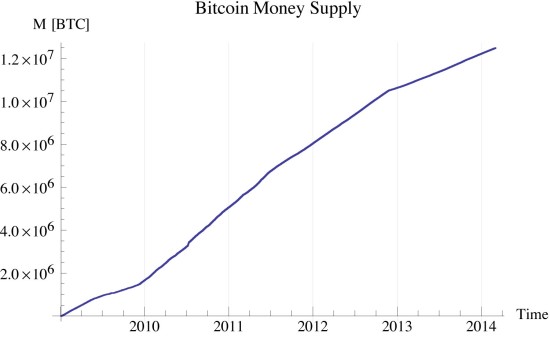
bitcoin money supply
The total number of satoshi is programmed into the source code and is solely a function of the block number (time). I used the average of each six block interval.
bitcoin temperature
The bitcoin temperature is computed by differentiating the specific entropy with respect to specific internal utility, leaving:
where is a positive constant of proportionality
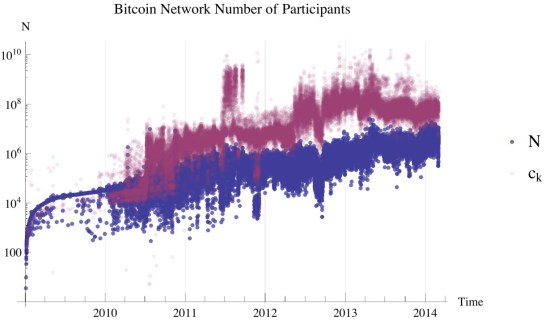
bitcoin participants
The number of bitcoin participants was calculated to a constant of proportionality by assuming that
Later, I will show how this assumption is justified as our model to this point does not incorporate into the entropic equation of state. Based on the definition of
, the number of participants reduces to,
When coupled with
we can compute the carrying capacity of the bitcoin network as:
Figure 6 shows the maximum entropic carrying capacity and the estimated number of bitcoin participants.
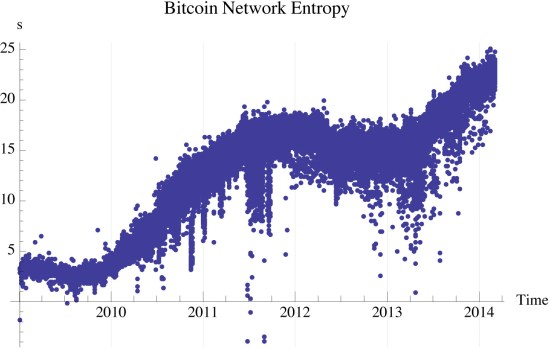
bitcoin entropy
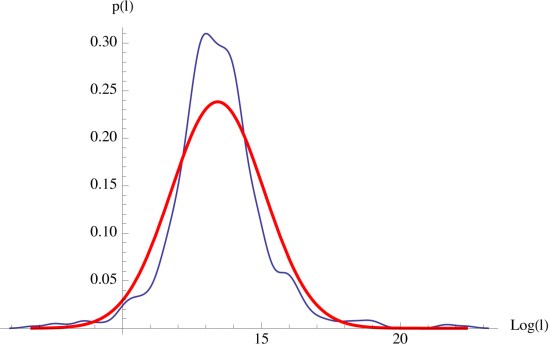
The entropy is computed in one of two ways, from the data directly or from the entropy derived form the model distribution. I estimate the former by dividing the transactions into 3 dB wide bins. Based on the range of transactions this is typically 40 bins. I then count the occupancy of each bin and divide by the total number of transactions to compute the probability of occupancy in each bin. I do same to the the CDF of the log-normal distribution, to compute it’s bin occupancy probability.
Please note that the negative entropy is due to measurement error, and is based upon its information theoretic definition physically impossible. I think the negative entropy here is due to the distribution of the marginal utility of transactions in those periods as not being constant as I assumed. I compute the differential entropy of the data distribution, figure 7, by:
The differential entropy of the log-normal distribution is:
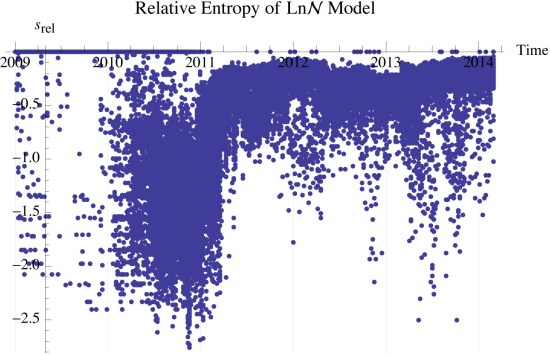
Using the bin data, I compute the relative entropy between the data and the model as,
Figure ?? shows the relative entropy between the model and the data. is a significant finding. We see in figure ?? that for the recent blocks
. This means the simple log normal model represents the data well, and that there are other unknown factors that influence the data beyond the model, but are not statistically significant.
We see that the entropy is mostly a function of the temperature and the relationship between the number of network participants and the structural capacity, . While the money supply has an impact, a different approach is needed to formally develop this understanding.
Empirical Modeling
We turn our attention to modeling the observed data and developing relationships for the extensive and intensive parameters. In the blockchain, we identified 4 logically independent variables: specific entropy, specific internal utility, marginal utility, and the z-parameter. We begin by assuming a simple functional relationship between these parameters.
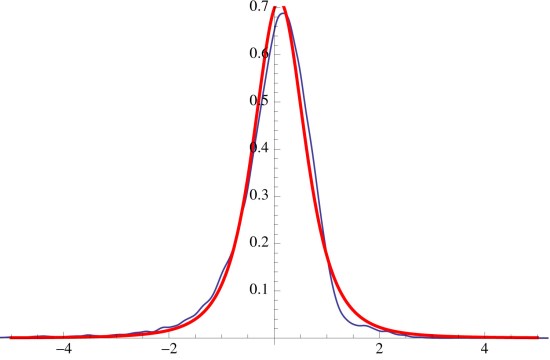
Using a MLE linear regression of the data since December 24, 2010 at 13:01:45 we find,
with residuals that follow in figure 9.
We find that our simple model explains the observed data quite well and is adequate for us to assess the as yet unquantified intensive parameters. This also allows us to derive the Maxwell relationships for bitcoin.
Conclusion
The work here provides additional insight into bitcoin. It presents a fairly complete picture. Some key observations are:
- The development of a measure of network participants
- The identification of a measure of marginal utility for bitcoin
- Understanding that it is possible to have deflation (falling prices) in a stable system,
while maintaining a stable network.
- We can see instances where the network became unstable (notably in 2011 after the first Mt Gox crash), the impact of Cyprus “bail-ins”, and the lack of network impact of the final crash of Mt Gox earlier this year.
- The methods developed here are easily adapted into SQL code and can be incorporated into existing blockchain API’s.
Data Files
All the data files can be found in this DropBox folder. If you have difficulty accessing this information have other comments/questions please post a comment on this page or contact me on twitter. Enjoy!
Eigenvalues and Other Exotic Beasts
This next part is a hypothesis. I do not have the knowledge or mathematical ability to prove/disprove it. So I’ll call it Cal’s conjecture. When I was playing around with the variable relationships, and I noticed that the characteristics of the variance of the log-normal distribution had some interesting properties that were eriely similar to the inverse of the fundamental eigenvalue. The discussion I am about to go into is regarding the Boltzmann transport equation in a multiplying media. The Boltzmann formalism and the formalism of Gibbs are used to describe and develop the same branch of science, statistical mechanics. In deriving and developing everything here, I used Gibbs’ formalism. It is not a branch of physics that I am familiar with so it took me a while to wrap my head around it. By training I am a nuclear engineer, we use the transport equation in everything that we do. It is the starting point of the entire set of mathematics and neumerical methods we use to describe a reactor. So I may be a little eigenvalue happy, but those things do have a tendency to pop up from time to time.
When we talk about neutron flux, we typically break the time evolution of the flux into two sets of equations, first is one that defines the spatial distribution, which we assume is time invariant to allow separability. I’m going to make the same mathematical abuse here. The other set of equations are a superposition of spatial modes called eigenfunctions. (Duderstadt and Hamilton 1976)
We tend to concern ourselves with the fundamental, asymptotic, form as the eigenvalues are ordered and the fundamental eigenvalue dominates the time evolution of the system.(Duderstadt and Hamilton 1976) This leaves us with,
When we substitute this into the diffusion model, we have:
Thinking of the variance of the log normal distribution, as the inverse of
we see much of the importance of the variance. in nuclear engineering we call the inverse of the fundamental eigenvalue,
. If k>1 the system is super critical meaning that it is creating its own growth. If
, the system is said to be critical or self sustaining. The critical configuration is very special, not only is it where we operate reactors at power, it is a maximum entropy configuration that is invariant to the the power (neutron density of the reactor). The other variable in the above equation
is the average neutron lifetime, how long a neutron spends bouncing around in the reactor from birth to loss (absorption or leakage). We can use a similar analogy here about the bitcoin “flux”, I don’t have a really good physical interpretation other than to call it the “bitcoin lifetime”. We let
and
Testing to see if this theory is even worth looking into we can descritize the above equation as
Solving for results in figure 10, where
for all recent (last 4-years) of transactions.
So maybe my hairbrained idea isn’t so out to lunch after all. Right now this is just a convenient observation that happens to give a profound result. Proving the deeper mathematical meaning is far beyond my skill set and leave that to another enterprising soul.
Looking at the residuals of figure 10 we have figure 11 which shows the lifetime as being lognormally distributed… and
.
We can talk about period but we are going to avoid this. If you are interested in what all this sort of kinetic junk means get a hold of a good reactor analysis text book I reccomend Duderstadt and Hamilton’s 1976 classic “Nuclear Reactor Analysis”. Almost all of the above discussion is from their text, pp 235 and 236. That chapter on reactor kinetics is perhaps the easiest to understand as any I’ve ever read. I’m a subject matter expert on reactor kinetics, my PhD thesis is on reactor kinetics. If your interested here’s my Proposal.
Implications of the Exotic Beasts
Ok, my head is hurting. I’m sure yours is too. I am almost done, I promise. We need to discuss the implications of on the growth and development of economies. This is very very important. Because after listening to economics podcasts for the last three years, a graduate course in micro economics, and just reading the news/watching the Fed, economics have no $%#@! idea what the hell they are talking about. I mean seriously, these jokers think that they can apply the powder of sympathy and fix the economy. ‘Come on! How full of $%&! can you be?
Economics can be a science. As it is practiced today, it is most definitely not. The Austrians call it a pseudoscience or scientism. And the Austrians aren’t above this either because they have all this great logic and then say the problem is with counting, you can’t count, if you count your one of them. Seriously?! Heaven forbid we actually use our brains and count stuff… BTW the theory that developed all of the above analysis is built off of counting. Science is about counting. More specifically, I define science as the study of reproducible events. No more and no less. This is also why I think that math is the language of science. Austrian economics is like Fight Club, “The first rule of Fight Club is that you don’t talk about Fight Club.” Golly guys can we grow up already?
My definition of science leaves plenty of room for what we know and what we don’t know. Science explains the stuff we observe and can reproduce. Religion explains everything else. They are not at odds with each other they are complementary and have distinct boundaries. I think people blur these boundaries to try and control those who can’t or don’t want to think. This goes for both sides of the argument too, the creationist lunatics say ignore what you can count, while the atheists say only the rational mind is important there is nothing else. Atheism is as much a religion as Catholicism, don’t let them fool you. Everything has boundaries and when we apply those assumptions outside of those boundaries then we cause problems.
We Are in Trouble, but bitcoin’s good and so is the World.
Growth. We are focused on Growth. Must. Have. Growth. I can hear the Kenysians chanting this now “supply side economics” “demand side economics”. Let’s print money lets give it away for shovel ready jobs. Lets give everyone healthcare it is a right. Raise minimum wage. Income Equality for all now! Government has a need to spy on its citizens. War is good for the economy. And on and on…
It is hard not to hear this silly prattle. It’s ubiquitous. We think that by restricting our action that we are doing well, by invading privacy, regulating specific outcomes we are doing what is best for society. We are not. That by redistributing wealth we make everyone better off. We do not. Figure 12 shows the Gini coefficient of several developed and formerly developed countries, see if you spot the similarities.
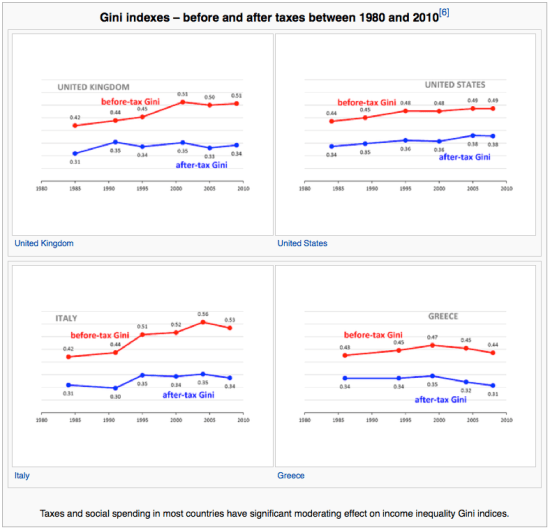
Figure 12: Gini Coefficient for various western countries (Source: Wikipedia)
Income distributions are log normal. There is a Lorenz Symmetry associated with a log-normal distribution too, but we will ignore that. A log-normal distribution that is critical, has a Gini coefficient of 0.521. if the Gini is less than that
meaning that the economy is sub-critical. If the Gini is > 0.521, the economy is super critical. Redistributing wealth makes the economy more sub critical. So how do we have economic growth in a sub-critical economy. Simple, we borrow from the future to pay for today. It’s called debt.
A sub-critical economy can only grow, when there is an outside source term of capital pumping money in. The farther the economy is away from criticality the larger the source has to be to create growth. The relationship here is quite simple. Using another definition of
Think of it as economic efficiency, We have a GDP in 2014 of x amount of dollars. Multiply it by and see what the “growth” would be if we didn’t have our wise and prescient government intervening by making our kids pay for our lifestyles today. Let’s take Greece as an example. In Greece, their Gini of .32 corresponds to a
. This means Greece policy is so effective that it takes 40% of the previous years GDP and throws it away. To get the GDP growth to look “normal” and not cause a default on their loans, they need to borrow 42% GDP to get a nominal growth rate. Please note, when I refer to GDP I am talking the REAL GDP not in fiat inflated value destroying currency, but no joke UTILITY not monopoly money.
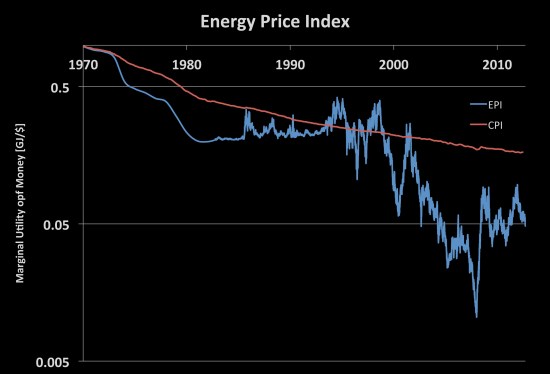
Speaking of monopoly money the central banks like making it look like they are creating growth in nominal terms. That ain’t growth it’s theft. They are taking value away from savers to give it to the financial sector. This is why whenever measuring utility always use a fixed reference point. I like using the price of primary energy. It’s a hard number to fudge and the governments haven’t figured out that they need to fudge it or suppress it to hide what they are doing, yet.
Let’s look at the US, Gini of 0.38 after tax and redistribution. The US has a . To get historic 3% growth we need to borrow 37% of the previous years GDP. That does not sound like a sustainable economic model to me. The scale of the problem for the US is much different. Our economy is $16 trillion compared to Greece’s $250 billion. This is roughly $6 trillion/year ($19,000/person-year) compared to $105 billion/year ($9,300/person-year). Which is more sustainable? Fortunately for us the actual burden is reduced because we are destroying our currency. This way we can appear to have historic growth by exerting much less work. Phew! Central banks make is so easy for us to grow. I mean really! This money printing makes us all better off… No not really. It actually reduces our action.
So how do we achieve criticality? How do we make our economy grow without having to borrow money? Simple, make less restrictive policy. This is not likely to happen because politicians are incentivized to maintain political rents so they can get reelected. Political rents do not contribute to our overall economy. Sorry Virgina, Santa ain’t real.
Bitcoin actually creates value from value. The rate is starting to taper out as feedback effects are starting to kick in as the bitcoin economy scales. But the fact when Satoshi Nakamoto greated a place without government and it has had a k>>1 for the last 4 years is amazing and shows the potential this protocol and currency have.
So what about the rest of the world why is there hope? Simple, there are still places in the world where policy is not so restrictive as to kill economic growth. The world has a . You can pick off the numbers from this graphic I used form the Bill and Melinda Gates Foundation 2014 letter.
Conclusion
I really am done here. I you didn’t get too upset at my destruction of the entire sum of economic growth theory or by my libertarian rants. If you have an issue with what I said or my analysis. Everything I used to develop it is here on this website. I was as careful as I could be and am sure I made some mistakes. However, when I applied my theory to actual data, the models just fell into place with the theory with the data. My proofs may be messy and incomplete, but their results are indisputable, you need to come up with a simpler model that explains everything that I did better than I did and more. You can also choose to ignore me. Fine go ahead. But if you think the bitcoin price volatility is an indication of insecurity, you are missing out on the biggest thing in a very very long time. I may be wrong, but you will be hard pressed to prove it.
I wish you good luck. I’m signing off of blogging for an indefinite period of time. I have other more important work (more important to me) that I need to focus my attention upon. This has been a fun project, I learned a lot. When I started, I still was a bit of a socialist. Now, any semblance of progressiveness is gone. I learned new math and taught myself economics. I see how complex systems can be easily understood in very broad terms. It has been wild. I see the world around me with the veil lifted. It is not pretty and it is hopeful. It is complex and beautiful.
I turn these ideas over to you. Whomever you are, I stand relieved. I understand what I need to, I’ve given you the tools and the framework to understand as I do in its depth, richness, and humility, as our knowledge is ultimately constrained and is more powerful than most anything that is out there. There is not a paradox between science and religion. It is like saying there is a paradox with a coin that has two sides. Each side is part of the coin, just as the known and the unknown are parts of our lives.


Always insightful, thanks!
Reblogged this on mashime.
0_o
He’s trying to predict the future based on his own attempt to create a theory of psychohistory by misapplying principals from physics to economics? I think we’ve hit peak libertarian.
I am not Hari Seldon and this is not psychohistory. I didn’t set out to prove anything when I started this project. I saw a problem that I wanted to understand. So, I went back to first principles, von Neumann and Morgenstern’s axioms of Game Theory and von Mises’ axiom of action, and used information theory to express the measure of our observations of the past. That’s it. No more, no less. I started this project as a progressive, I ended it as a libertarian. The understanding I gained changed my perspective.
Whether you use this theory or not, its up to you. I’m not going to force it upon you. I will alert you to the consequences. First, if you maintain your current world view, everyone who does adopt this theory is going to eat your lunch. Second, if you don’t want people to eat your lunch then you need to develop a theory that explains our past observations better than what I did here. In the second case, if I don’t adopt your better and improved theory everyone that adopts yours will eat my lunch. I like to eat, so whichever theory explains our observations the best and provides useful understanding of the future, then that is the theory I will adopt even if that means abandoning the work that I did here.
My question to you is, “Do you like to eat, too?”
Wow! I came here by way of OurFiniteWorld. Thanks for posting the link and this work. I haven’t looked at the physics of nuclear reactors since 1972, so I am waaaay behind on all this and I haven’t touched an eigenvector for years.
I’ve some modelling that suggests that the present money system (and that includes bitcoin) is fundamentally broken. But you probably know that already.
It is a breakthrough to have a specific theory relating criticality, wealth distribution and growth, though there are unanswered questions about unlimited exponential expansion.
best wishes for whatever you are doing today.
Richard,
Sorry about the delay in my response. I’m interested in what you’ve done for modeling if you want to talk about it. It is a trip down memory lane every time I hear Eigenvalue, German speaking TA’s can make Eigen sound scary… I’m interested in why you think bitcoin is broken. As for fiat currencies, yes they work, but aren’t adequately constrained to have meaningful longevity.
Using the reactor analogy, growth in the neutron population occurs until the feedback effects; temperature, xenon, doppler, void coefficient, pressure, radial/axial expansion, etc all kick in to reduce k_eff to 1. There are many decades (factors of 10) of reactor power where the power can rise exponentially based solely on the excess reactivity. A k_eff=1 is where the entropy of the reactor is maximized based on the constraints it has (control rod position, core inlet temperature, FP poisons, and physics). Our society functions in a similar statistical manner, just our constraints are a little different. I think we are a long way away from reaching the physical [energy] limitations of the planet. In the short term, we may hit the limitations of the current political and social constraints. I think in many ways, with the level of unrest and tension, that we are close to this point.
Cal: I thought I will inform you about http://bpeconomics.org/. We have something going on there on Statistical Economics. Ram Poudel
As usual, another bitcoin article assuming that bitcoin encompasses all distributed cryptocurrencies. Bitcoins are not a monopoly and their market power will get weaker as time goes along.
This is not a bitcoin only method. It is restricted to a single currency because that is the only data contained in the blockchain. I applied this technique to traditional fiat, USD. So the approach is very general. Please do not feel restricted in what can be analyzed.
I mentioned in the original post that I used bitcoin abe v 0.9. This parser can access many different blockchains of a slew of currencies. You can import these into MySQL or other such DB and then analyze the data using the MatLab files I provided. If you are so inclined you can adjust the bitcoin abe source code to do the analysis that I did. It is nothing more complicated than addition, multiplication, logarithms, and their associated inverse functions.
I am not going to do the analysis of these currencies. If you are interested in doing this work I encourage you post your analysis and results here on this site. My intention with this site is for it to be a forum for the discussion and analysis of many different things using and further developing the formalism that I presented here.
I just showed what can be done and how to do it. My time is limited and I have many other projects I am associated with, so my restricted scope is a result of my restricted time. Thank you for reading and you are more than welcome to participate.
Pingback: Bitcoins: Made in China | Bitcoin Market
Pingback: Bitcoins: Made in ChinaUnlicoin.com | Unlicoin.com
Pingback: Bitcoins: Made in China | Bitcoin Trading Room
Pingback: Bitcoins: Made in China : REPORTCOIN
Pingback: Bitcoins: Made in China | Much Doge News .comMuch Doge News .com
Pingback: Bitcoins: Made in Chin
Pingback: Bitcoins: Made in China Bitcoin Magazine
Pingback: Bitcoins: Made in China – Bitcoin Magazine